Problem of the Week #84: Monday March 31st, 2025
As before, these problems are the results of me following my curiosity, and I make no promises regarding the topics, difficulty, solvability of these problems.
Please register for an account if you would like to join the discussion below or share your own problems.
This problem was inspired by Round 2 of the 1972 British Math Olympiad, Q1
Let’s arrange all 3 digit binary codes in a list starting with 000 such that each code differs from its previous code by only 1 digit.
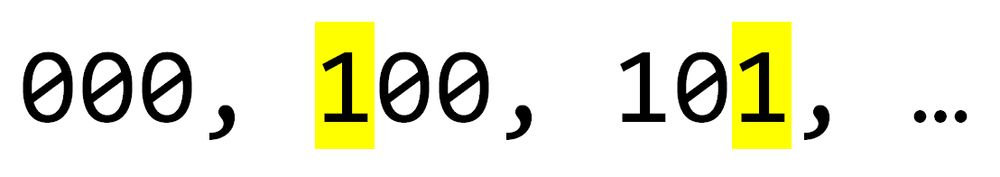
a). Find one such arrangement of 3 digit binary codes.
b). If we arrange all 3 digit binary codes in a list, starting with 000, such that each code differs from its previous code by only 1 digit, is it possible for 101 to be the last code on the list?
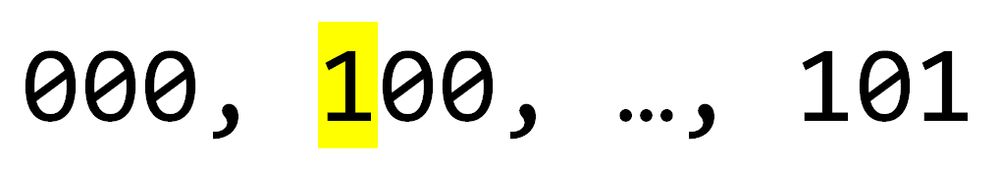
c). How many ways are there to arrange all 3 digit binary codes in a loop, starting with 000, such that each code differs from its previous code by only 1 digit (including the first and last codes)?
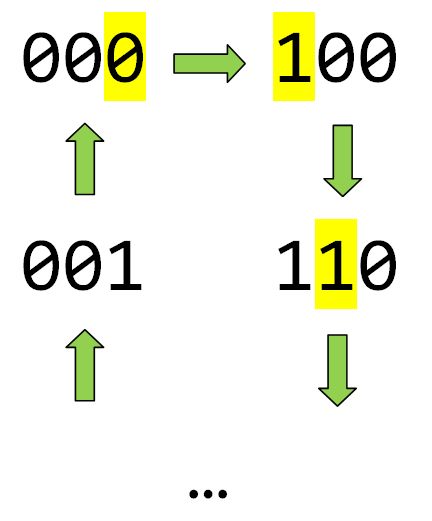
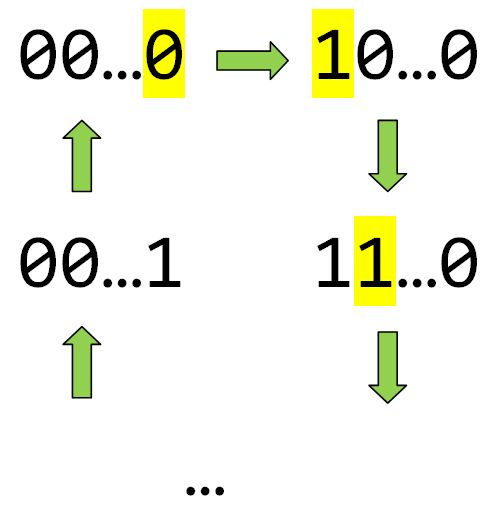
d). Prove that we can always arrange all n digit binary codes in a list starting with all 0s such that each code differs from its previous code by 1 digit.
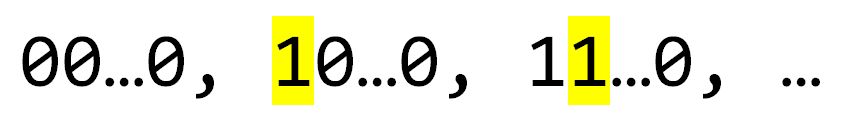
e). Find all possible last codes if we arrange all n digit binary codes in a list starting with all 0s such that each code differs from its previous code by 1 digit.

f). How many ways are there to arrange all n digit binary codes in a loop, starting with all 0s, such that each code differs from its previous code by only 1 digit (including the first and last codes)?
g). Share your own problem inspired by this one.

h). Give one of these questions to a friend/colleague/student/family member to start a mathematical discussion.
