Problem of the Week #79: Monday February 3rd, 2025
As before, these problems are the results of me following my curiosity, and I make no promises regarding the topics, difficulty, solvability of these problems.
Please register for an account if you would like to join the discussion below or share your own problems.
This problem is inspired by the 1973 USAMO Q1.
Let’s consider the 3D version of regular planar angles, called solid angles. If an angle can be thought of as a portion of a full circle, then a solid angle is a portion of a full sphere.
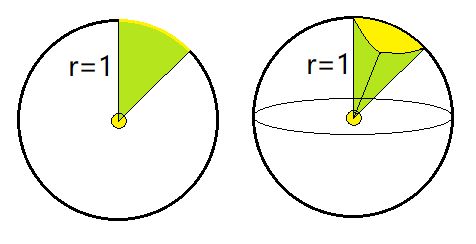
a). An angle that takes up a full circle is 2π units (ie. radians). By the same token, how many units should we make a solid angle that takes up a full sphere?
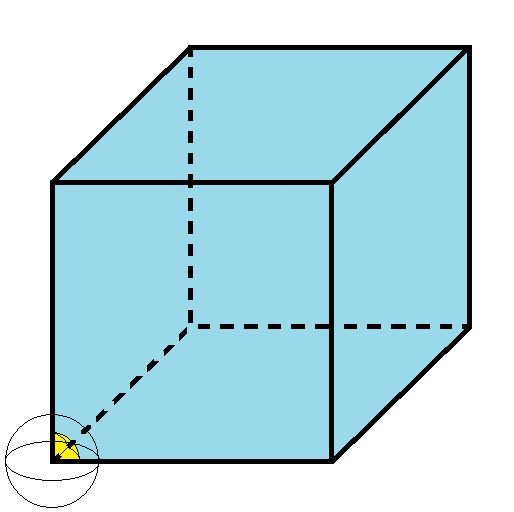
b). Using the same unit we developed in the previous question, how big is the interior solid angle at a vertex of a cube?
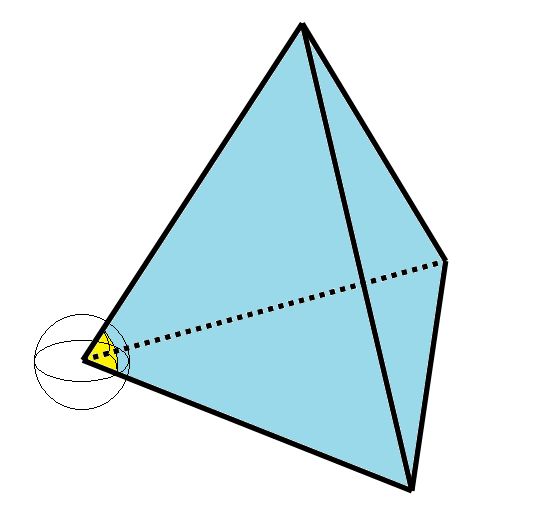
c). What fraction of a sphere does a vertex of a regular tetrahedron take up? (Or roughly how many regular tetrahedrons can we fit around a point?)
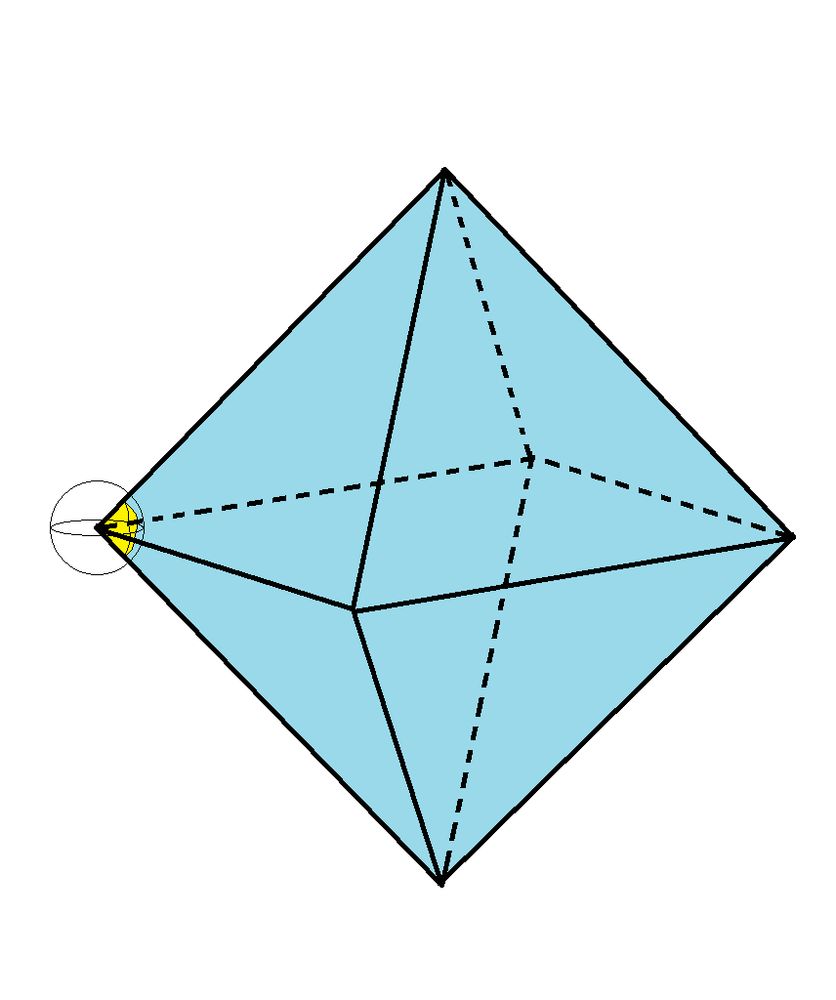
d). What fraction of a sphere does a vertex of a regular octahedron take up? (Or roughly how many regular octahedrons can we fit around a point?)
e). All triangles have the same interior angle sum of π units (radians). Do all tetrahedrons have the same interior solid angle sum?
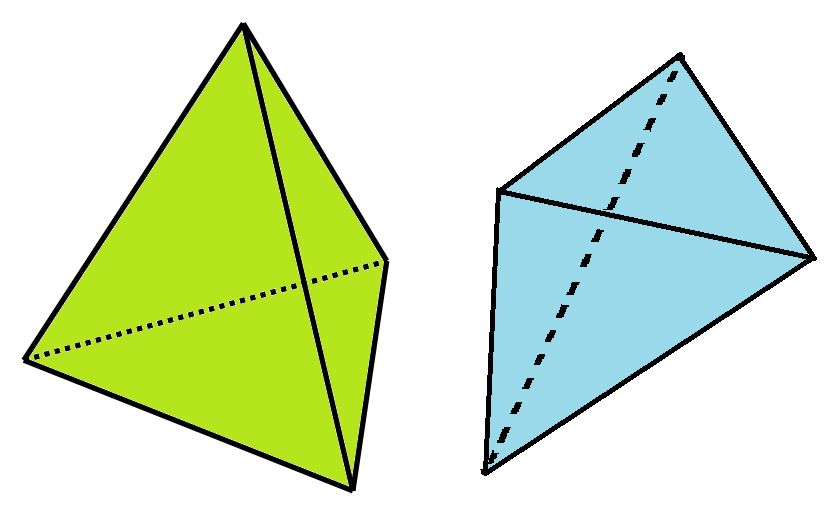
f). What’s the maximum possible the interior solid angle sum of a tetrahedron? What’s the minimum?
g). Share your own problem inspired by this one.

h). Give one of these questions to a friend/colleague/student/family member to start a mathematical discussion.
