Problem of the Week #90: Monday June 2nd, 2025
As before, these problems are the results of me following my curiosity, and I make no promises regarding the topics, difficulty, solvability of these problems.
Please register for an account if you would like to join the discussion below or share your own problems.
This problem is inspired by the 1973 Canadian Math Olympiad, Q7.
A pronic number is a natural number of the form n(n+1), where n is also a natural number. Let’s call the reciprocal of a pronic number a pronic fraction.
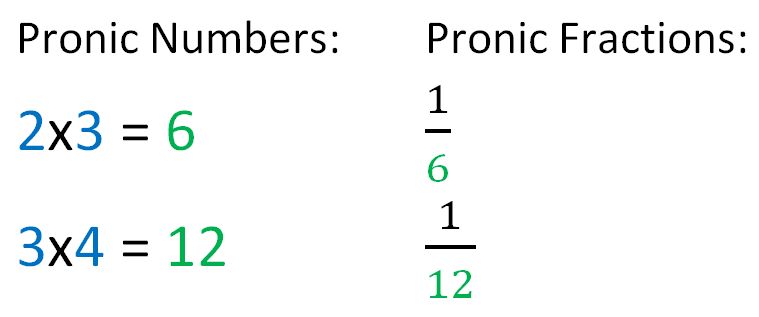
a). Prove that every pronic fraction is the difference of 2 consecutive unit fractions.
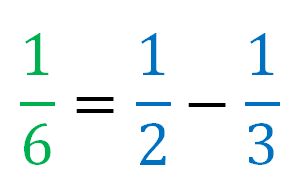
b). Write 1/4 as the sum of distinct pronic fractions.

c). How many ways are there to write 1/4 as the sum of distinct pronic fractions?
d). How many ways are there to write 1/4 as the sum of consecutive pronic fractions?

e). Can every unit fraction be written as the sum of distinct pronic fractions?

f). Can every unit fraction be written as the sum of consecutive pronic fractions?
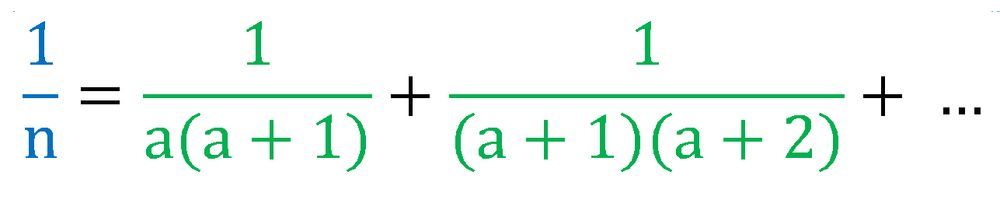
g). Share your own problem inspired by this one.

h). Give one of these questions to a friend/colleague/student/family member to start a mathematical discussion.
