Problem of the Week #85: Monday April 7th, 2025
As before, these problems are the results of me following my curiosity, and I make no promises regarding the topics, difficulty, solvability of these problems.
Please register for an account if you would like to join the discussion below or share your own problems.
This problem is inspired by the 1971 Canadian Math Olympiad Q7.
a). Which are there more of, 2-digit numbers that are divisible by their 10s digit, or 2-digit numbers that are divisible by their unit digit?
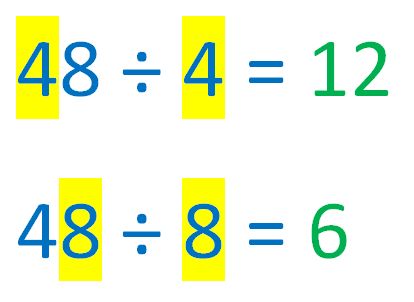
b). Which are there more of, 3-digit numbers that are divisible by the 2-digit number made of their first two digits, or 3-digit numbers that are divisible by the 2-digit number made of their last two digits?
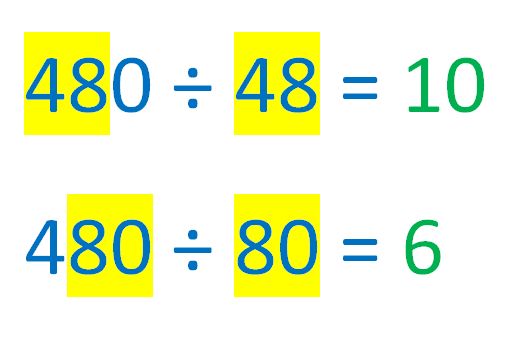
c). How many 3-digit numbers are divisible by the 2-digit number made by removing their 10s digit?
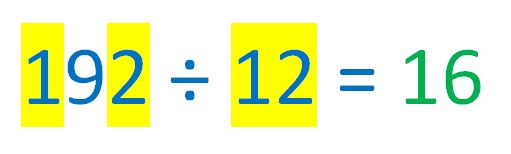
d). How many 4-digit numbers are divisible by the 3-digit number made by removing their 10s digit?
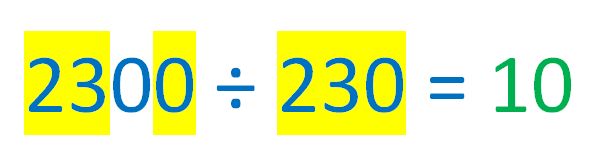
e). How many 4-digit numbers are divisible by the 3-digit number made by removing their 100s digit?

f). Notice all 4-digit numbers divisible by the 3-digit number made by removing their 10s digit end in 00, but not true if we remove the 100s digit instead. Which digit can we remove from an n-digit number such that all that are divisible by the resulting number would end in 0s?
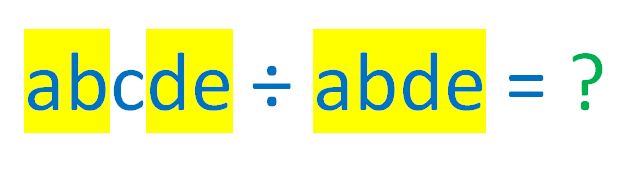
g). Share your own problem inspired by this one.

h). Give one of these questions to a friend/colleague/student/family member to start a mathematical discussion.
