Hi there, I've taken about a half year break because I was feeling a bit stressed over coming up with new problems every week. I'm back though, and this time a bit more prepared with having a steady source of inspirations.
Problem of the Week #50: Monday June 17th, 2024
As before, these problems are the results of me following my curiosity, and I make no promises regarding the topics, difficulty, solvability of these problems.
Please register for an account if you would like to join the discussion below or share your own problems.
This problem is inspired by this twitter post.
Consider the subtraction game that goes like this: Write down one whole number at each corner of the square below, then fill in each side with the positive difference the two neighbouring corners and connect the four new numbers in a smaller square. Repeat the subtraction to continue forming new squares in the middle.
a). Does this game always end with four 0s in a square no matter what numbers you start with?
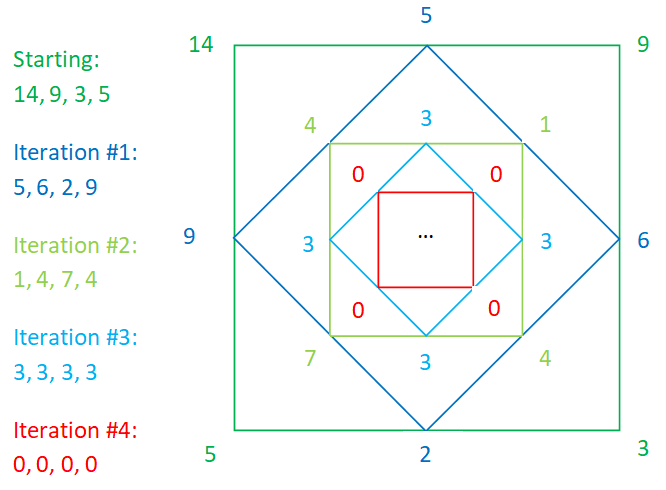
b). The example above takes 4 iterations to get to all zeros. If we are given a limit on how big the starting numbers are, say less than or equal to 20, how do we find the combination that takes the most number of iterations to get to all zeros?
c). Now consider the same game but with more sides in the starting polygon (a triangle or pentagon, etc. instead of a square). For which numbers of sides does the polygon always reduce to all zeros? What do the other polygons do?

d). For the cycles that do not end in all zeros, does it always reduce to a combination of just one other number and zero? For example, this set of starting numbers ends in a cycle of just 1s and 0s.

e). For a given arrangement of starting numbers, how do we predict the ending non-zero number? For example, the set above ends in 1s and 0s, but some might end in 2s and 0s or 5s and 0s.
f). For a given number of sides in the polygon, how many different ending cycles are there? For example, for pentagons there are two possible ending cycles:

g). For a given number of sides in the polygon, how do we find the longest ending cycle? For example, for pentagons the longest ending cycle is 3 iterations long, as shown above on the right.
