Problem of the Week #87: Monday April 21st, 2025
As before, these problems are the results of me following my curiosity, and I make no promises regarding the topics, difficulty, solvability of these problems.
Please register for an account if you would like to join the discussion below or share your own problems.
This problem is inspired by the 1975 USAMO Q1.
The floor function [a] denotes the greatest integer less than or equal to a. For x and y strictly between 0 and 1, the probability of [2x]+[2y] being 1 is 1/2:
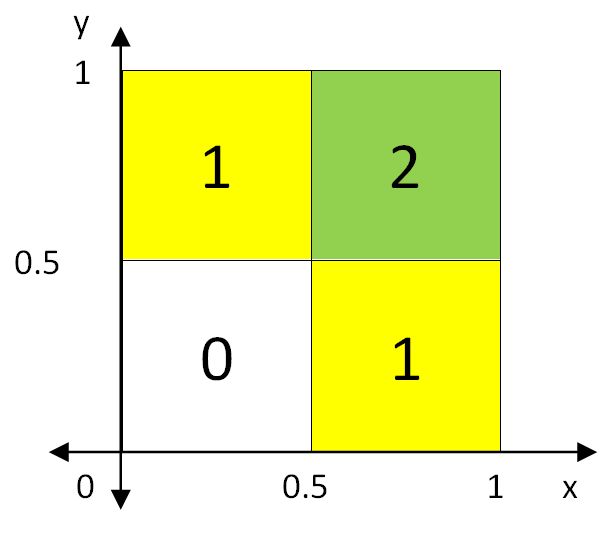
a). If we choose x and y randomly between 0 and 1, what’s the probability that 2[x+y] is 0? 1? 2?
b). If we choose x and y randomly between 0 and 1, what’s the probability that 2[x+y] less than [2x]+[2y]? Equal to? Greater than?

c). If we choose x and y randomly between 0 and 1, what’s the probability that [2x+y] + [2y+x] is 0? 2? 3?

d). If we choose x and y randomly between 0 and 1, what’s the probability that [2x+y]+[2y+x] is less than [3x]+[3y]? Equal to? Greater than?
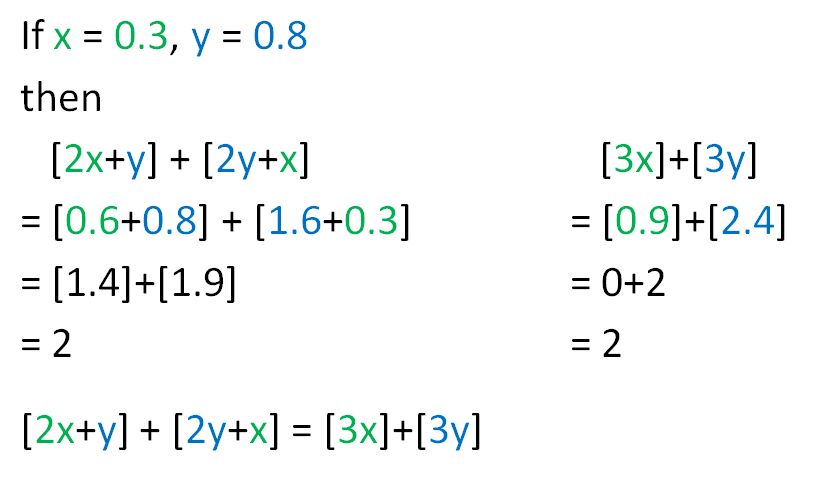
e). If we choose x and y randomly between 0 and 1, what’s the probability that 2[1.5x+1.5y] is less than [3x]+[3y]? Equal to? Greater than?

f). If we choose x and y randomly between 0 and 1, for a positive integer k, what’s the probability that 2[(k/2)x+(k/2)y] is less than [kx]+[ky]? Equal to? Greater than?
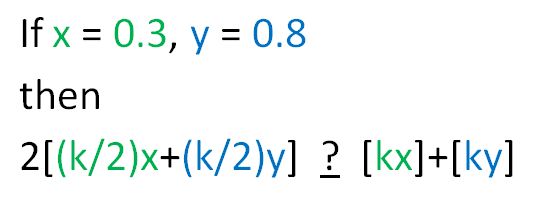
g). Share your own problem inspired by this one.

h). Give one of these questions to a friend/colleague/student/family member to start a mathematical discussion.
