Problem of the Week #86: Monday April 14th, 2025
As before, these problems are the results of me following my curiosity, and I make no promises regarding the topics, difficulty, solvability of these problems.
Please register for an account if you would like to join the discussion below or share your own problems.
This problem is inspired by the 1971 Canadian Math Olympiad Q9.
If we draw pairs of circles of the same sizes centered at two distinct points and mark where each pair of circles intersects, we’d trace out a straight line.
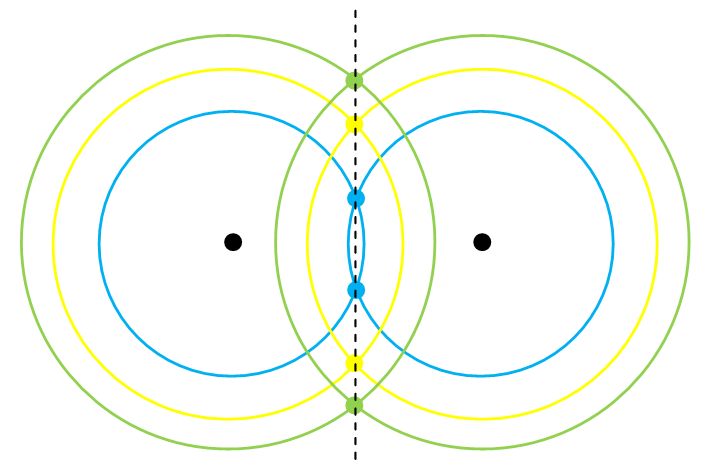
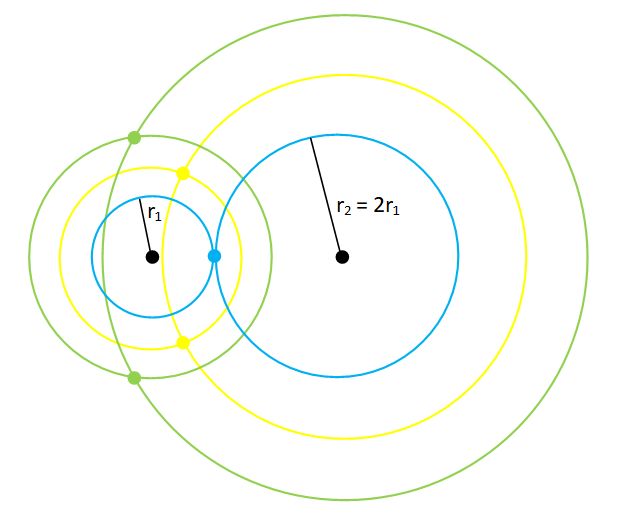
a). What shape would we trace out from the intersection points if one radius is always 2x the other radius?
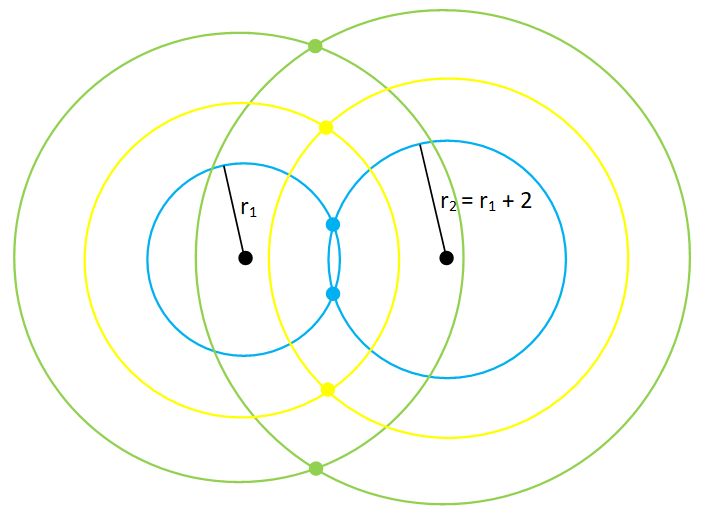
b). What shape would we trace out from the intersection points if one radius is always 2 units larger than the other radius?
c). What relationships between the radii would trace out an ellipse from the intersection points?
d). What relationships between the radii would trace out a hyperbola from the intersection points?
e). What relationships between the radii would trace out a parabola?
f). What changes to the relationships between the radii would allow us to move or stretch the shapes trace out from the intersection points?
g). Share your own problem inspired by this one.

h). Give one of these questions to a friend/colleague/student/family member to start a mathematical discussion.
