Problem of the Week #91: Monday June 9th, 2025
As before, these problems are the results of me following my curiosity, and I make no promises regarding the topics, difficulty, solvability of these problems.
Please register for an account if you would like to join the discussion below or share your own problems.
This problem is inspired by the 1974 British Math Olympiad Round 2, Q3.
Also consider this an extension of the Line Stitching problem.
a). Sketch the area reachable by the midpoint of a line segment of length 1, if its entire length is confined to the first quadrant (x>=0 and y>=0) of a Cartesian plane, and one of its end points must be on the x- or the y- axis.
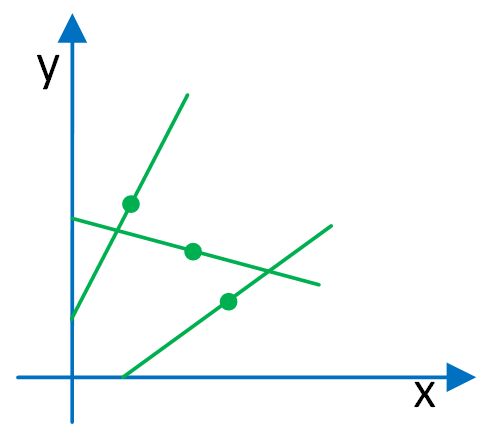
b). If a line segment of length 1 must have one end point on the x-axis and the other on the y-axis, what shape does its midpoint trace out? Prove your claim without using algebra. (You might want to use your findings from part a.)
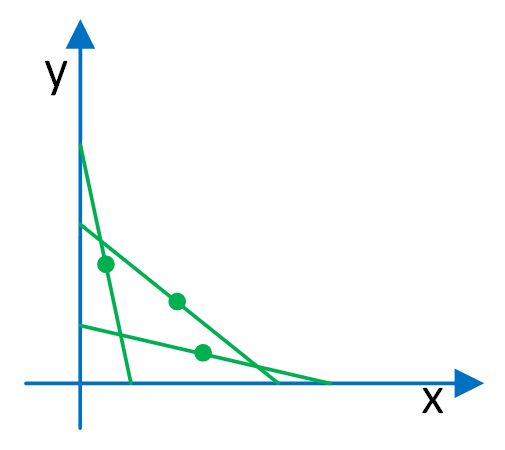
c). Sketch the area reachable by the center of an equilateral triangle of side length 1, if its entire area is confined to the first quadrant (x>=0 and y>=0) of a Cartesian plane, and one of its vertices must be on the x- or the y- axis.
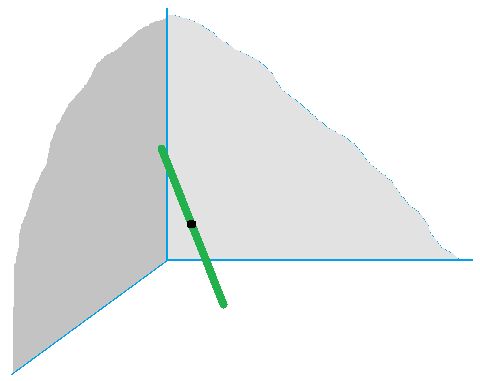
d). Sketch the space reachable by the midpoint of a rod of length 1 if it’s leaning against the corner of a room (2 walls and a floor, all meeting at right angles. One endpoint of the rod touches the floor. The other touches at least one of the walls).
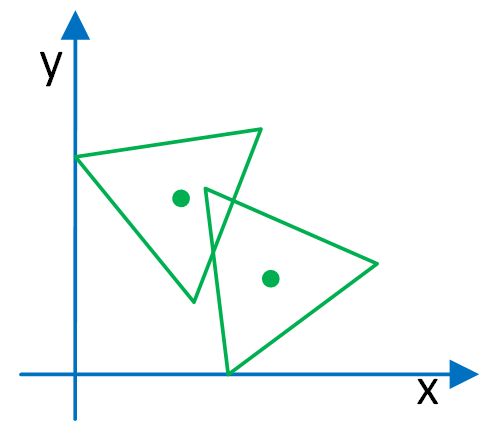
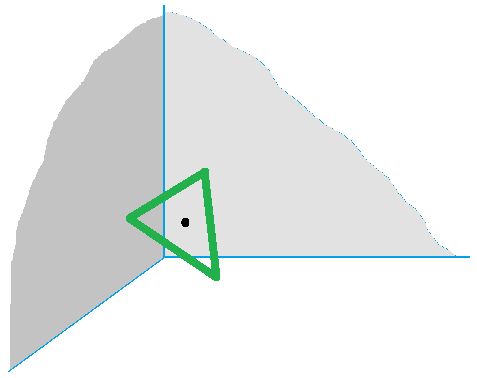
e). Sketch the space reachable by the center of an equilateral triangle of side length 1 if it’s leaning against the corner of a room. (2 walls and a floor, all meeting at right angles. The triangle touches the floor and at least one wall.)
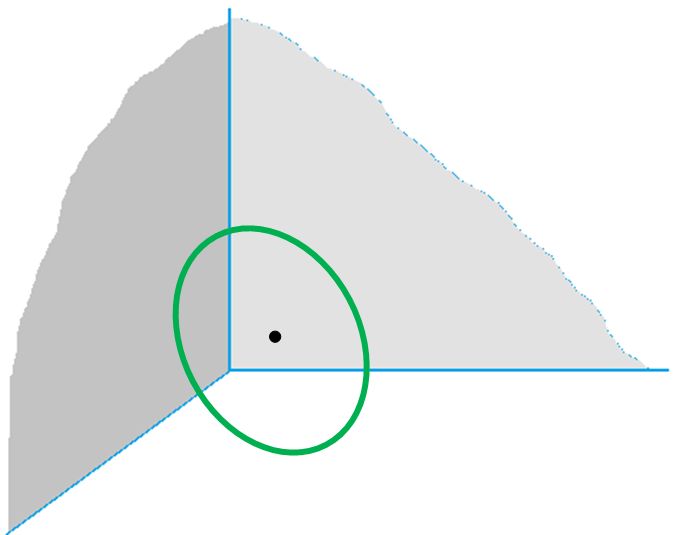
f). Sketch the space reachable by the center of a circle of radius 1 if it’s leaning against the corner of a room. (2 walls and a floor, all meeting at right angles. The circle touches all 3 surfaces.)
g). Share your own problem inspired by this one.

h). Give one of these questions to a friend/colleague/student/family member to start a mathematical discussion.
