Problem of the Week #82: Monday February 24th, 2025
As before, these problems are the results of me following my curiosity, and I make no promises regarding the topics, difficulty, solvability of these problems.
Please register for an account if you would like to join the discussion below or share your own problems.
This problem is inspired by the 13th Problem of the Week.
Flipping the switch of one light in this chain of connected lights will change the state (on O or off X) of the corresponding light (highlighted) and its immediate neighbours.

a). Continue flipping switches until all lights in the example are on.
b). Is there a starting state of the 4 connected lights where we cannot turn all of them on?
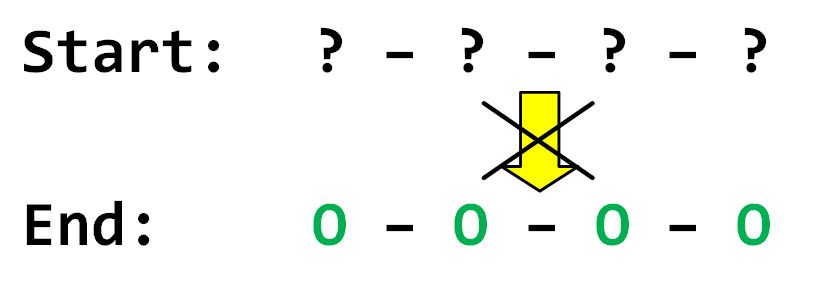
c). Prove that i) to turn on all lights with the fewest number of switch flips, each switch can be flipped at most once, and ii) the order of the switch flips makes no difference to the end state of the lights.


d). Is there a starting state of 5 connected lights in a row where we cannot turn all of them on?
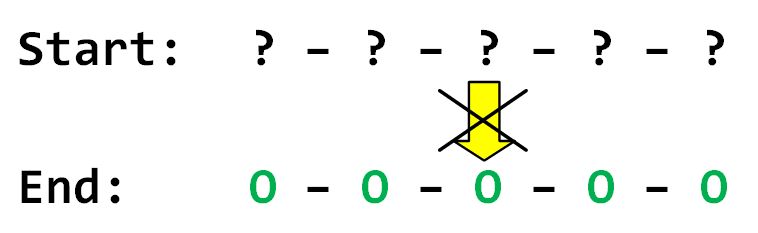
e). Starting with k connected lights in a row all turned off, if there are 2 distinct ways (different sets of switch flips) to turn on them all with the fewest number of flips, prove that there is at least 1 starting state of the lights where we cannot turn on all of them.

f). For which natural numbers k is it always possible to turn on all k lights connected in a row regardless of their starting states?
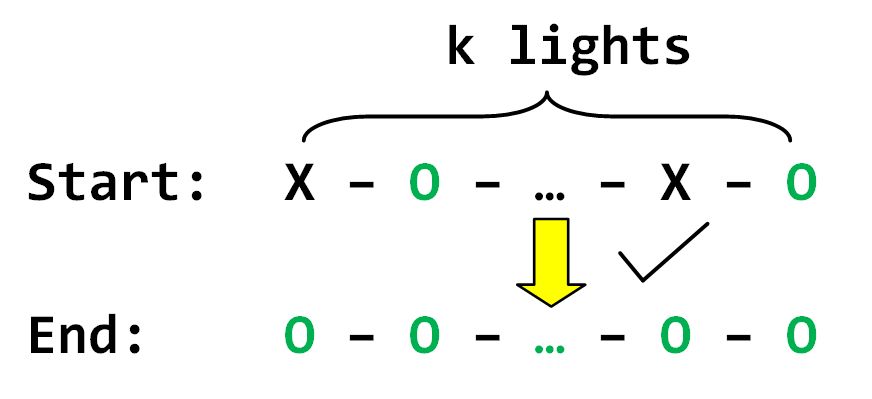
g). Share your own problem inspired by this one.

h). Give one of these questions to a friend/colleague/student/family member to start a mathematical discussion.
