Problem of the Week #78: Monday January 27th, 2025
As before, these problems are the results of me following my curiosity, and I make no promises regarding the topics, difficulty, solvability of these problems.
Please register for an account if you would like to join the discussion below or share your own problems.
This problem is inspired by the 1970 Canadian Math Olympiad Q10.
Consider expanding this expression:

a). Is it possible for a, b to be integers, c, d non-integers, and f(x) to have all integer coefficients?
b). Is it possible for a, b, c, d to all be non-integers, and f(x) to have all integer coefficients?

c). Is it possible for a, c to be integers, b, d non-integers, and f(x) to have all integer coefficients?

d). Is it possible for a=c=1, b, d non-integers, and f(x) to have all integer coefficients?

e). Is it possible for a=c=1, exactly one of b and d to be an integer, and f(x) to have all integer coefficients?

f). What are the necessary and sufficient conditions on a, b, c, and d for f(x) to have all integer coefficients?
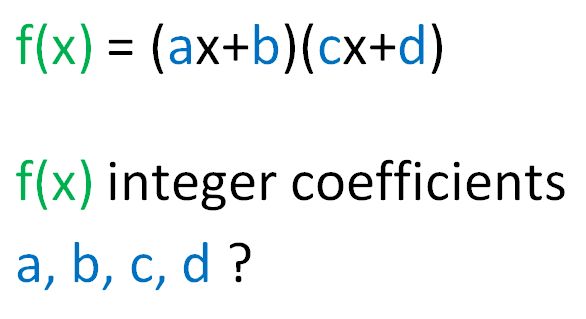
g). What are the necessary and sufficient conditions on polynomial expressions g(x) and h(x) for their product f(x) to have all integer coefficients?

h). Share your own problem inspired by this one.

i). Give one of these questions to a friend/colleague/student/family member to start a mathematical discussion.
