Problem of the Week #72: Monday November 18th, 2024
As before, these problems are the results of me following my curiosity, and I make no promises regarding the topics, difficulty, solvability of these problems.
Please register for an account if you would like to join the discussion below or share your own problems.
This problem is inspired by AIME 1984 #12.
Starting with some points on a number line, if we put a mirror somewhere on the number line, it will reflect all existing points in itself so that the resulting set of points are symmetrical around it.

a). Starting with a point at 1, find all points on the number line if we put a mirror at 2 and another one at 5.
b). Starting with a point at 1, where should we put the mirrors if we want a point at each prime number under 30?

c). Starting with a point at 1, how many ways are there to put in mirrors so that we have a point at each prime number under 30?
d). Starting with one point at 1, how many mirrors are needed to guarantee that we have a point at each element of a set of n real numbers?

e). Starting with a point at (1, 1) on a Cartesian plane, how many mirrors do we need to result in a point at each lattice point if mirrors can be any straight lines of any slope?
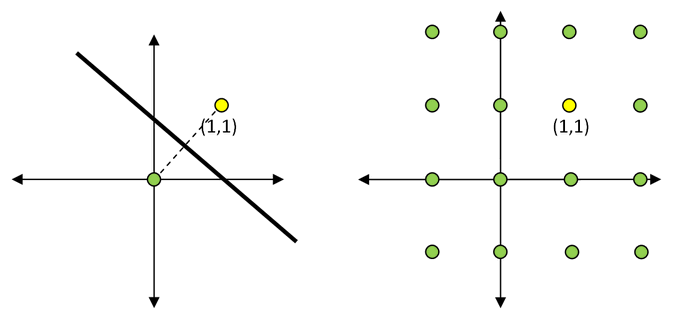
f). Starting with a point at (1, 1) on a Cartesian plane, how many mirrors do we need to result in a point at each lattice point if mirrors are any points and can reflect in any direction?

g). Share your own problem inspired by this one.

h). Give one of these questions to a friend/colleague/student/family member to start a mathematical discussion.
